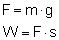Ten rodzaj energii mechanicznej mają ciała, które znajdują się na pewnej wysokości. I tu pojawia się problem z określeniem miejsca od którego liczymy tę wysokość.
Załóżmy że znajdujemy się w bloku w oknie na czwartym piętrze i "przez przypadek" wypadają nam dwie doniczki przez okno. Oznaczmy je odpowiednio A i B. Nasz sąsiad mieszkający pod nami (trzecie piętro) w złym momencie wyjrzał przez okno i jego głowa znalazła się na drodze doniczki A. Nasz drugi sąsiad także znalazł się w złym miejscu o niewłaściwej porze bo akurat spacerował po chodniku i "spotkał się" z doniczką B. Zastanówmy się czy obaj odczuli te spotkania tak samo? Która doniczka spowodowała większe szkody? Czy A, która przeleciała jedno piętro, czy B która przeleciała przez 4 piętra.

Pomyślmy przez chwilę o energii potencjalnej grawitacji doniczek przed wypadkiem. Mimo iż obie doniczki znajdowały się na czwartym piętrze, to łatwo się domyśleć, że ich energia potencjalna względem sąsiada mieszkającego pod nami była troszkę mniejsza niż względem tego który szedł po chodniku. Dlatego jeżeli mówimy, o energii potencjalnej grawitacji ciała to musimy sami wybrać względem którego poziomu liczymy wysokość na jakiej znajduje się to ciało. Najczęściej takim poziomem jest powierzchnia ziemi, lub np. podłoga w naszym pokoju, rzadziej głowa naszego sąsiada.
Spróbujmy teraz wyprowadzić wzór na energię potencjalną grawitacji ciała znajdującego się na wysokości h.

Postąpimy jak z energią kinetyczną, czyli obliczymy pracę potrzebną na wyniesienie ciała na wysokość h. Jeżeli wynosimy to ciało ruchem jednostajnym prostoliniowym to musimy zadziałać siłą F, która zrównoważy ciężar. Siła ta będzie równa co do wartości ciężarowi ciała, czyli:
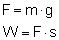
Droga w tym przypadku jaką musi przebyć ciało wynosi h. Zmieńmy więc nasz wzór: